CVP_to_SVP

From CVP to SVP

1 SVP问题

svp问题(Shortest Vector Problem），顾名思义，就是在格中寻找”长度“最短的向量。

将抽象的问题定量分析，我们可以把格中的一个点设置为坐标轴0点。这样可以把问题转化为：找到距离 0 点最近的格点

一般而言，我们使用向量的欧几里得范数作为“距离”的定义。

定义：对于维向量的欧几里得范数为

对于维的格，因为一个格基由条向量组成，相应的就会有条最短的向量。

下图展示了一个2维的最短两条向量

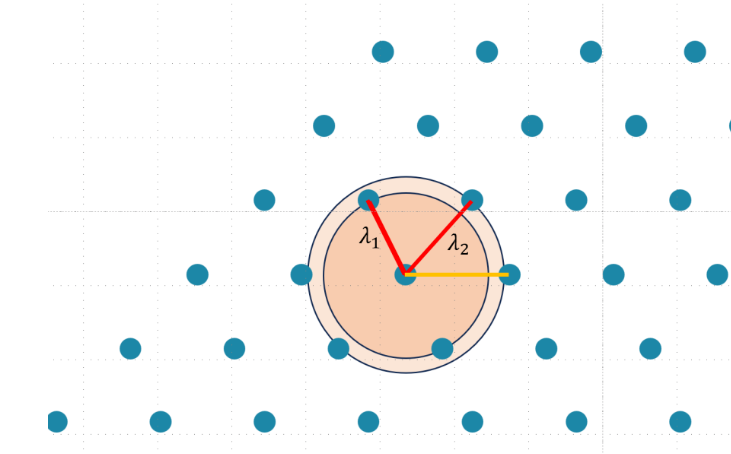
二维的SVP问题可以画同心圆来求解，但是如果维度上去了作图就行不通了。

但是，如果我们可以拿到相互正交的基格，那么我们只需要遍历基格中的各个向量就可以找到最短的向量了。

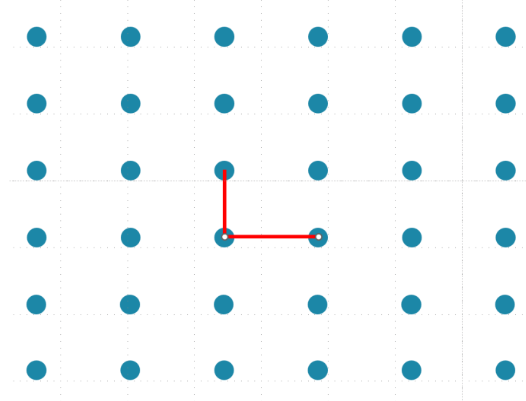
为了找到最短的向量，就要尽量使基格正交。

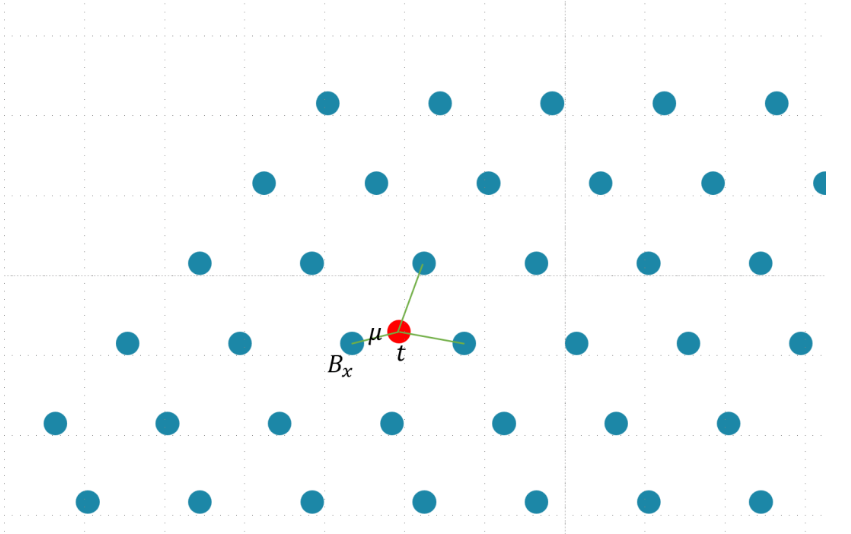
2 CVP问题

Lattice中另一大问题就是最近向量问题（CVP，Closest Vector Problem）了。问题的定义是这样的：给定连续空间中任意的一个点 ，找到距离这个点最近的格点 。

​ 其余包括还有 SIVP问题（Shortest Independent Vectors Problem）,BDD（Bounded Distance Decoding）问题 ,ADD（Absolute Distance Decoding）问题 等都是 SVP, CVP 的衍生，可以搞出如下的关联性

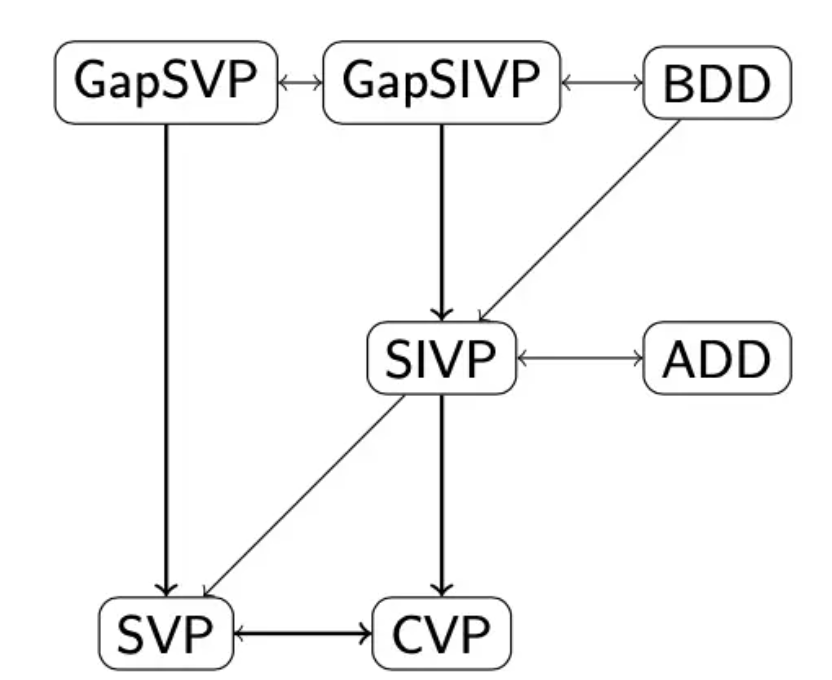
CVP-->SVP

假设我们有一个一维的格，然后我们需要找到距离点最近的格点

我们可以将格点”升维“，使得也成为新格的一个格点。

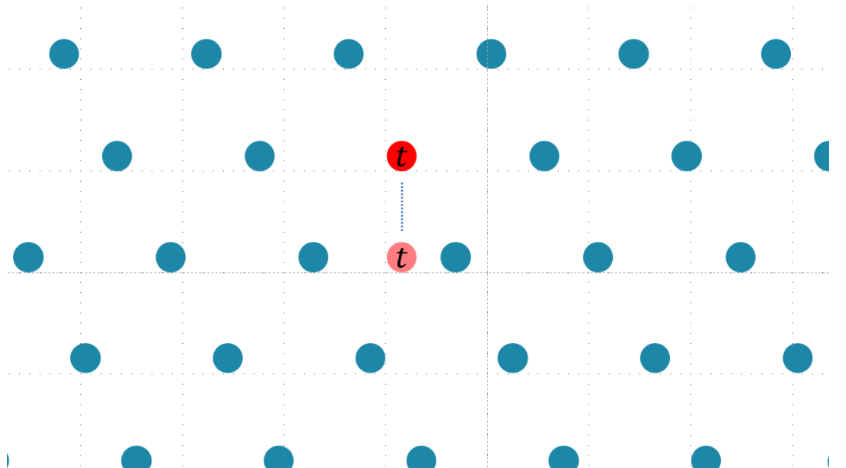
接下来，在这个新格中我们解决一下 SVP，找到最短向量，然后再将这个最短向量投影回原来的低维中，我们就能找到原来格中距离最近的格点了。

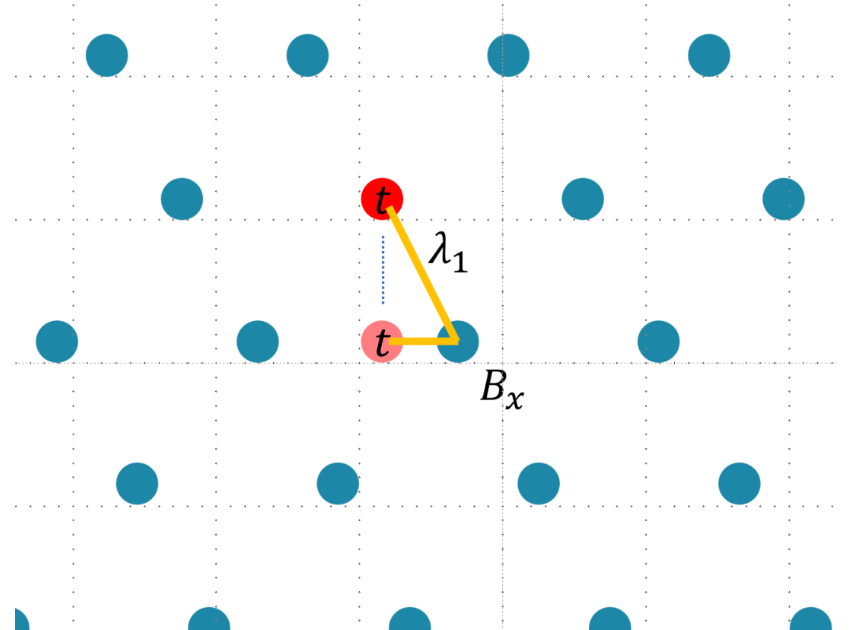
这样，CVP问题能够转化为SVP问题，而解决SVP问题的关键还是找到正交基

3 Gram-Schmidt基格正交化

事实上，由于“离散”的特性，我们仅可以通过对格基进行一系列（系数为整数）的线性变换找到接近正交的基，而这一过程，我们称为格基规约（Lattice Basis Reduction）

这里我们先介绍一种在线性代数中会学到的规约方法，即 Gram-Schmidt正交化，方便起见，我们在二维格上进行演示。

假设我们拥有一组基

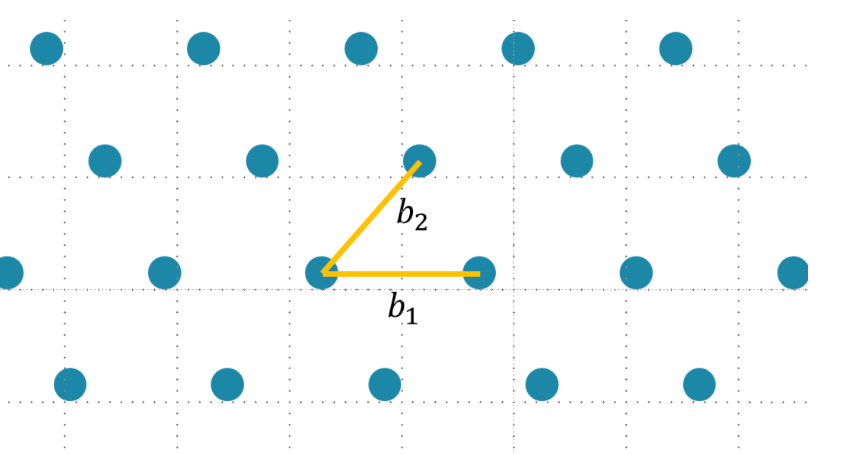
在这个Lattice中，这两个基向量是不垂直的。接下来，我们尝试找到一组互相垂直的基满足 $b_1^\perp b_2^b_1^*= b_1b_2^*$

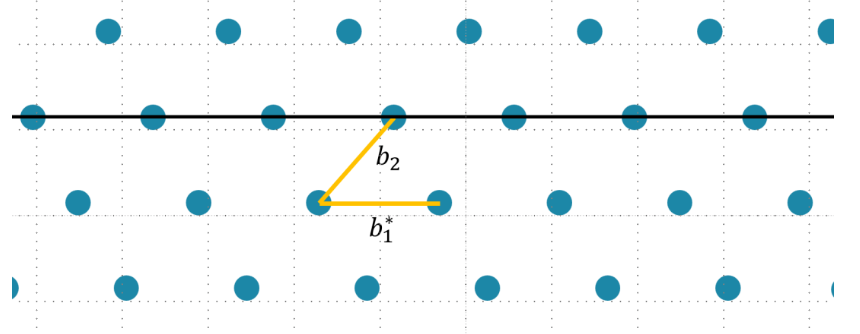
显然 ，不过由于在格上我们仅可以通过对格基进行一系列系数为整数的线性变换我们最终所能得到的尽可能“垂直“的格基

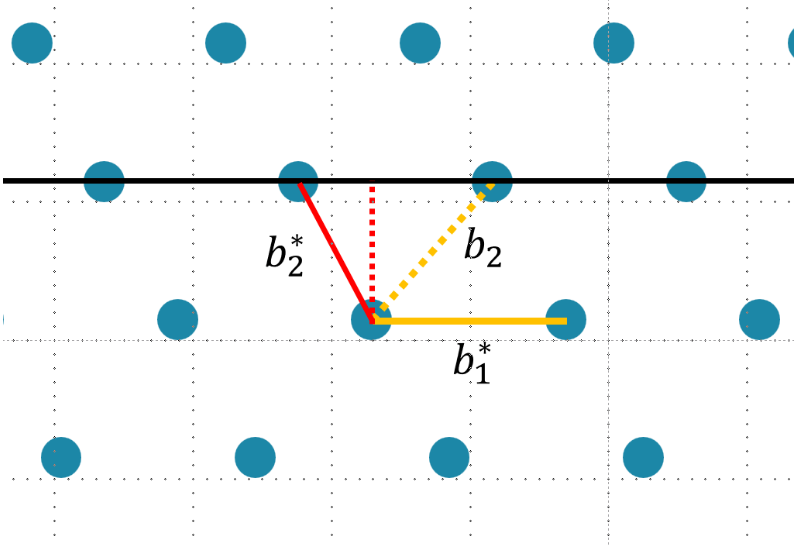
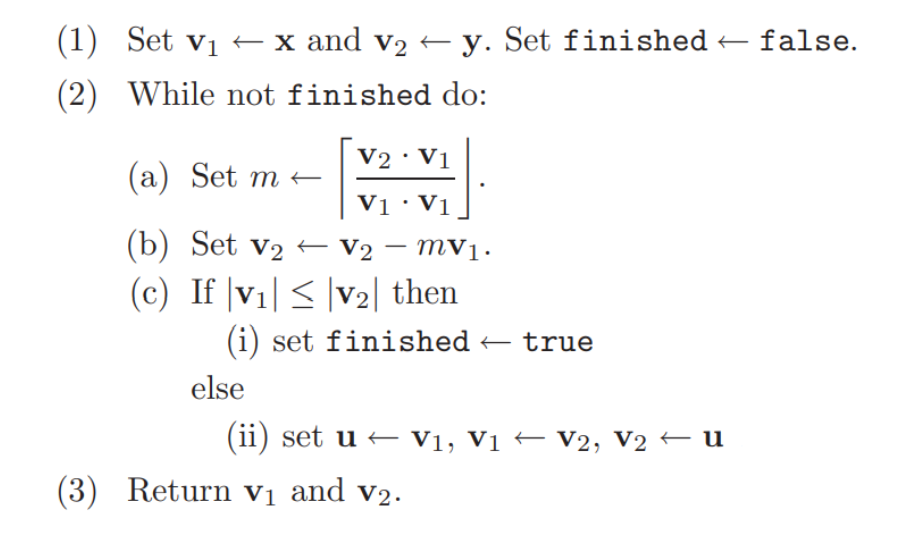
高斯算法中蕴含的思想与欧几里得算法类似，两者都是不断地实施先约化后交换的策略。在伪代码中，**(2)(b)是约化步，(2)(c)是交换步**。

不停地让两个向量互相约化，直到它们无法变得更短为止

低维

#sage
def Gauss(x,y):
    # step 1
    v1 = x; v2 = y
    finished = False
    # step 2
    while not finished:
        # (a)
        m = round(( v2.dot_product(v1) / v1.dot_product(v1) ))
        # (b)
        v2 = v2 - m*v1
        # (c)
        if v1.norm() <= v2.norm():
            finished = True
        else:
            v1, v2 = v2, v1
    
   return v1, v2

高维（LLL算法）

def max(a, b):
    return a if a > b else b

def LLL_v0(M, delta=0.75):
    B = deepcopy(M)
    Q, mu = B.gram_schmidt()
    n, k = B.nrows(), 1
    
    while k < n:
        
        # size reduction step
        for j in reversed(range(k)):
            if abs( mu[k][j] ) > 0.5:
                B[k] = B[k] - round( mu[k][j] ) * B[j]
                Q, mu = B.gram_schmidt()
        
        # swap step 
        if Q[k].dot_product(Q[k]) >= (delta - mu[k][k-1]^2) * Q[k-1].dot_product(Q[k-1]):
            k = k + 1
        else:
            B[k], B[k-1] = B[k-1], B[k]
            Q, mu = B.gram_schmidt()
            k = max(k-1,1)
    
    return B 

Reference：

1. 格基规约算法：算法详解-CSDN博客
2. (https://mp.weixin.qq.com/s/nzFRgOUkffeUaF9PqtEnQA )
3. Lattice学习笔记02：格中难题 - 知乎 (zhihu.com)